Hashing

Let’s say you have a string, such as "SPAM", and you’re trying to find if that string is contained in a list of a thousand other strings.

To do that, you’ll need to compare "SPAM" with as many as one thousand other strings. That’s a lot of comparing.

To compare two strings without hashing, you have to go character by character. Only if each character is the same can we say the two strings are identical.

/// Naive string comparison.
bool checkIdentical(String a, String b) {
  if (a.length != b.length) return false;
  for (var i = 0; i < a.length; i++) {
    if (a.codeUnits[i] != b.codeUnits[i]) {
      return false;
    }
  }
  return true;
}

That’s a lot of work! Imagine comparing whole paragraphs of text to each other. If only we could simplify this!

14 . 1 The idea

You know what’s easy to compare? Numbers. In fact, comparing whether two numbers are identical is a single instruction for the CPU. That is to say, it’s very fast.

Could we represent these strings as numbers?

Well, each character is a number, right? For the computer, A is 65, B is 66, C is 67, and so on. That’s called the “char code”—the internal representation of a character in the computer’s memory.

We could just take those numbers and use some mathematical formula to combine them into a single number.

And voilá: we have a way to encode a string of any length into a single number. That’s hashing. For a given string (like "SPAM"), that number will always be the same (305), no matter who or when does the computation. That is to say, it’s not a randomly assigned identification number: it can be recomputed at will.

/// Naive hashing function.
int hashString(String a) {
  var hash = 0;
  for (var character in a.codeUnits) {
    hash += character;
  }
  return hash;
}

Let’s come back to our original example of checking if a long list of strings contains "SPAM" in it. We can hash each of the thousand strings, and so now we have a list of numbers. A list of hash codes. This new list of numbers takes a lot less space in memory, is easier to sort, and faster to work with.

Success!

14 . 2 A small problem

Not so fast. Isn’t it possible to have two different strings with the same hash? After all, a string can be arbitrarily long, while a simple integer cannot.

In fact, with our naive hashing function above, the probability that there will be a hash collision is high:

if (hashString("SPAM") == hashString("MAPS")) {
  // Uh oh!
}

Remember, we’re just adding numbers together. Two plus three is the same as three plus two, which is the same as one plus four. Our program will not work as intended. It will insist that different strings are identical. Things will break.

This is why real hashing functions are a lot more involved than the naive one above. Even the simple CRC32 “checksum” is quite a few lines of bitwise operations and table lookups. The pseudocode for the popular SHA-1 hashing function is 46 lines long.

Using real hashing functions, the hash code of "SPAM" definitely isn’t equal to the hash code of "MAPS". Problem solved, right?

Not so fast. Even with non-trivial hashing functions, there can be collisions. The probability is small, but it’s there. Look at this table from Jeff Preshing’s blog:

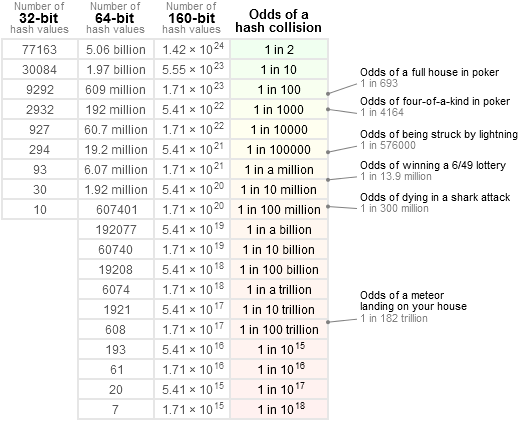
No matter how great your hash function is, if it only produces 32-bit hash codes, and you have a list of 77,163 unique strings, the probability that two of the strings have the same hash code is 50%. That’s not good.

Thankfully, hash functions that ship with modern programming languages use 64-bit hash values, and you’d need a list of over 5 billion strings to reach the 50% chance of collision. And with cryptographic functions like the aforementioned SHA-1, you’d need over one septillion (10²⁴) strings. Which is a lot.

14 . 3 Hashing is everywhere

If you’re using a modern programming language, hashing is working for you all the time. When you compare two strings, like with "spam" == "SPAM", that’s done via hashing in the background. When you create a map (also known as ‘dictionary’ in some languages), chances are it’s really a “hash map”: the keys of the map are represented by their hash codes.

I explained hashing on strings, but it applies to any data. You can hash vectors, sets, arbitrary classes or booleans. You can even hash numbers!

If you’ve used git, you are probably aware of git commit hashes. Like this:

$ git log
commit c2ae38f8a70d51dd003d137d4fff06f9eb4d1647
Author: Filip Hracek <some@example.com>
Date:   Thu Oct 29 11:46:33 2020 -0700

    Fix bug

That c2ae38f8... value is a hash code that uniquely identifies that commit. It’s just a very big number, written in hexadecimal. In decimal, it’s this:

1,111,429,502,104,458,606,634,325,828,610,920,458,897,444,378,183

The fact that git can describe any file—and any state of your project—with just one number makes it fast and powerful. Hashing enables git to be what it is: a version management powerhorse.

14 . 4 The name

The reason we say “hashing” and “hash function” comes from the ordinary use of the words “hash”.

When you hash potatoes, you chop them into tiny pieces and mix those pieces together. The structure of the original potatoes is lost, but they’re all in that final product.

When you hash strings, you chop them into bytes and mix those bytes together into a single number. The structure of the original string is lost, but the bytes are all represented in the final product.

14 . 5 Try it

Here’s a challenge for you, if you’re up to it. You have a class that represents a pair of integers: (x, y). Without researching the best approach on the internet, try to come up with a hash function. You’re trying to make sure that (2, 3) has a different hash code from (3, 2), and that (1, 0) has a different hash code from (-1, 0) or (0, -1). It’s harder than you may think. Here’s a DartPad for you.

As soon as you find a hashing function that looks promising, try to break it. Try to find two vectors that will result in the same hash code.